Introduction
Logistic Regression is a classification model where the output is discrete values like predicting whether a mail is spam or not, handwritten digit classifier, etc.
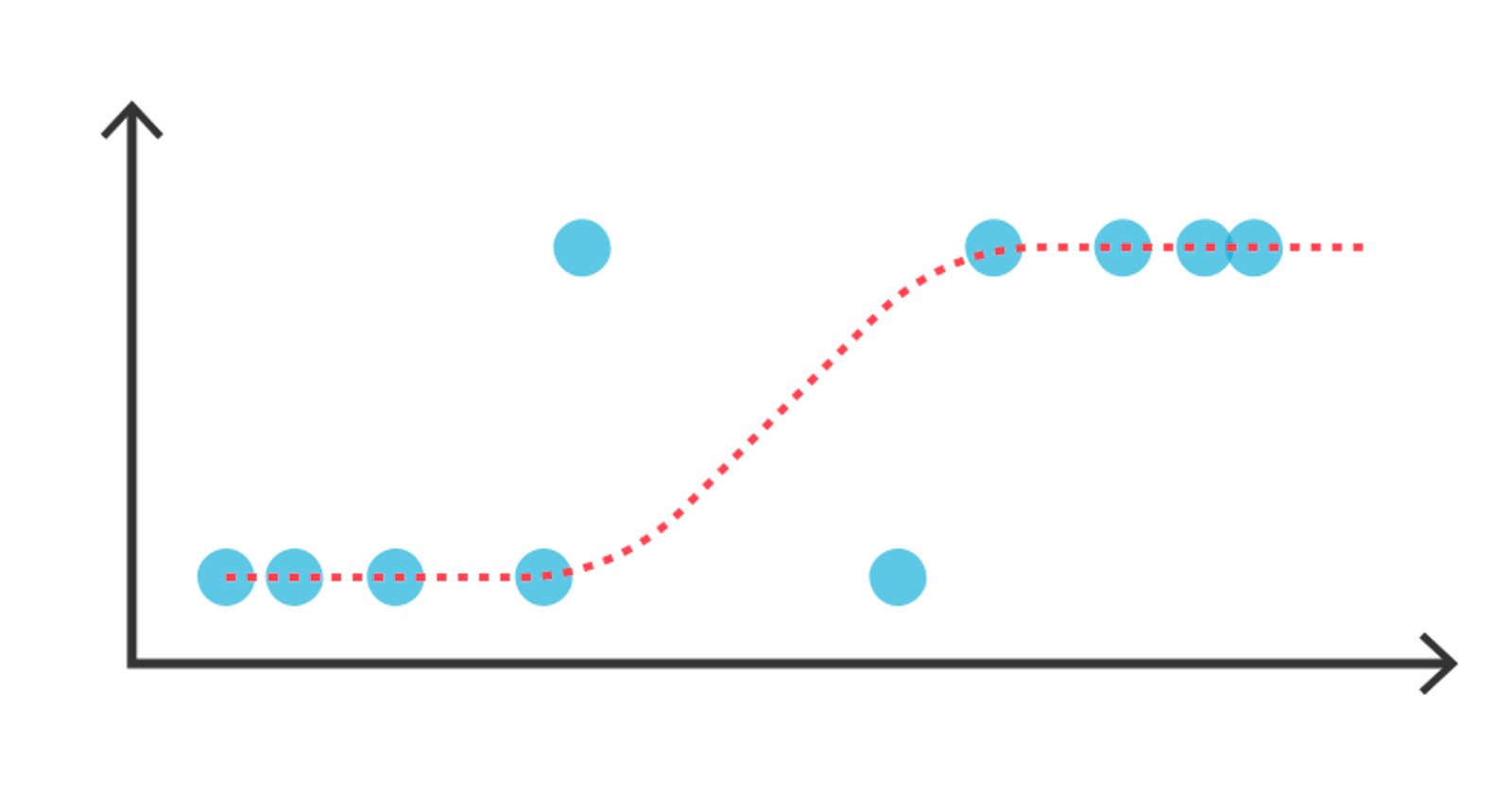
Problem with Linear Regression as a classification model
Suppose we have a dataset and our linear regression model generated its best fit line for it. Now if we add another data point (row) in our dataset, the model will shift our line to fit this point. If there is a shift in the line then the minimum threshold value for classifying the data changes. So in the beginning, the threshold might be 0.5 but after adding few more data points the value might become 0.8. This affects the accuracy of our model.
Hypothesis
Logistic Regression is built on top of our Linear Regression hypothesis. Recall our linear regression hypothesis function -
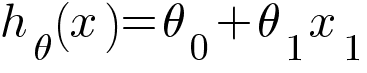
Since we are dealing with binary classification problem where the output could only be either 0 or 1, we need to limit the extreme values our hypothesis function could generate. This is done with the help of sigmoid function.
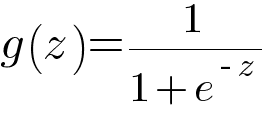
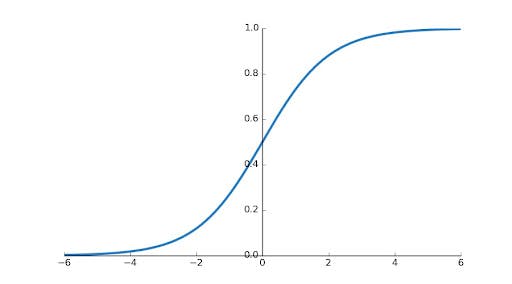
Graphically, sigmoid function looks like this -
Replacing z in the sigmoid function with linear hypothesis, we get -
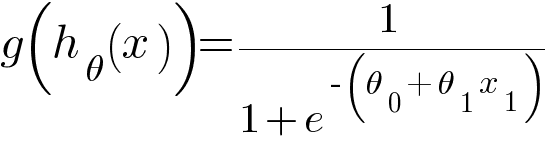
This is the hypothesis function for Logistic Regression Classifier. The values of this function will be between 0 and 1. The threshold value will be 0.5.
Loss Function
We used Mean Squared Error as our loss function for linear regression model but MSE doesn't work well for classification problems because it doesn't penalize as much as we want in case of misclassification. Also it will result in non-convex cost function with lot of local minima which is a very big problem for Gradient Descent algorithm to compute the global minima. Binary Cross Entropy is the loss function for Logistic Regression model.
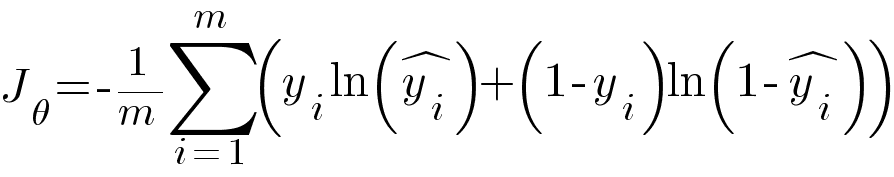
Where ŷ is the predicted value and y is the true value.
Optimizer
We use the same Gradient Descent algorithm as our optimizer to calculate the parameters with the only difference of hypothesis function in it. We calculate the partial derivative of our loss function with respect to weights and accordingly update the values of our weights.
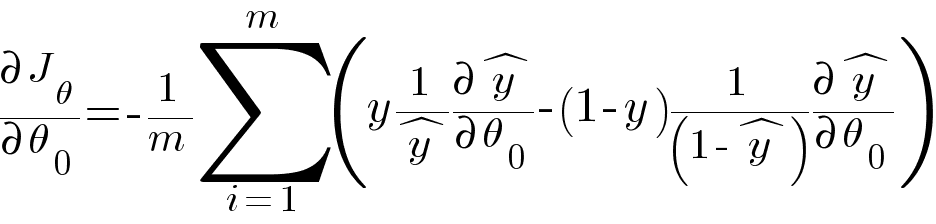
Calculating the partial derivative of ŷ and simplifying the equation we get -
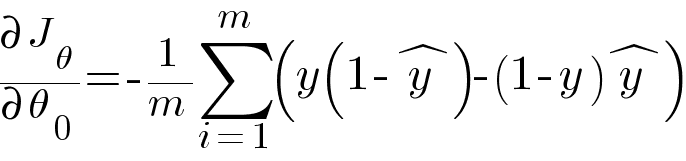
Similarly, partial derivative of loss function with respect to θ1
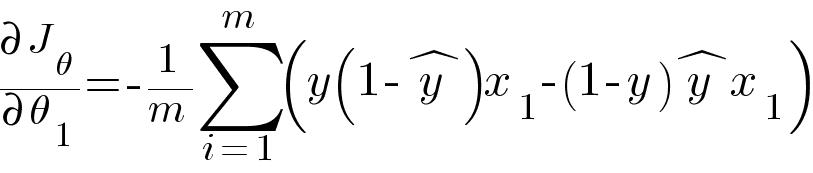
Then we update the values of θ0 and θ1 with the same equation like the one in Linear Regression.
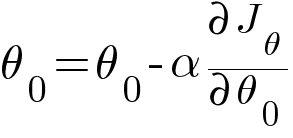
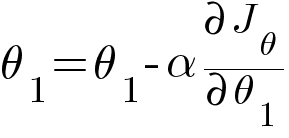
Where α is the learning rate.
Code
I have used iris dataset from sklearn to train my model.
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)
model = LogisticRegression()
model.fit(X_train, y_train)
model.score(X_test, y_test)