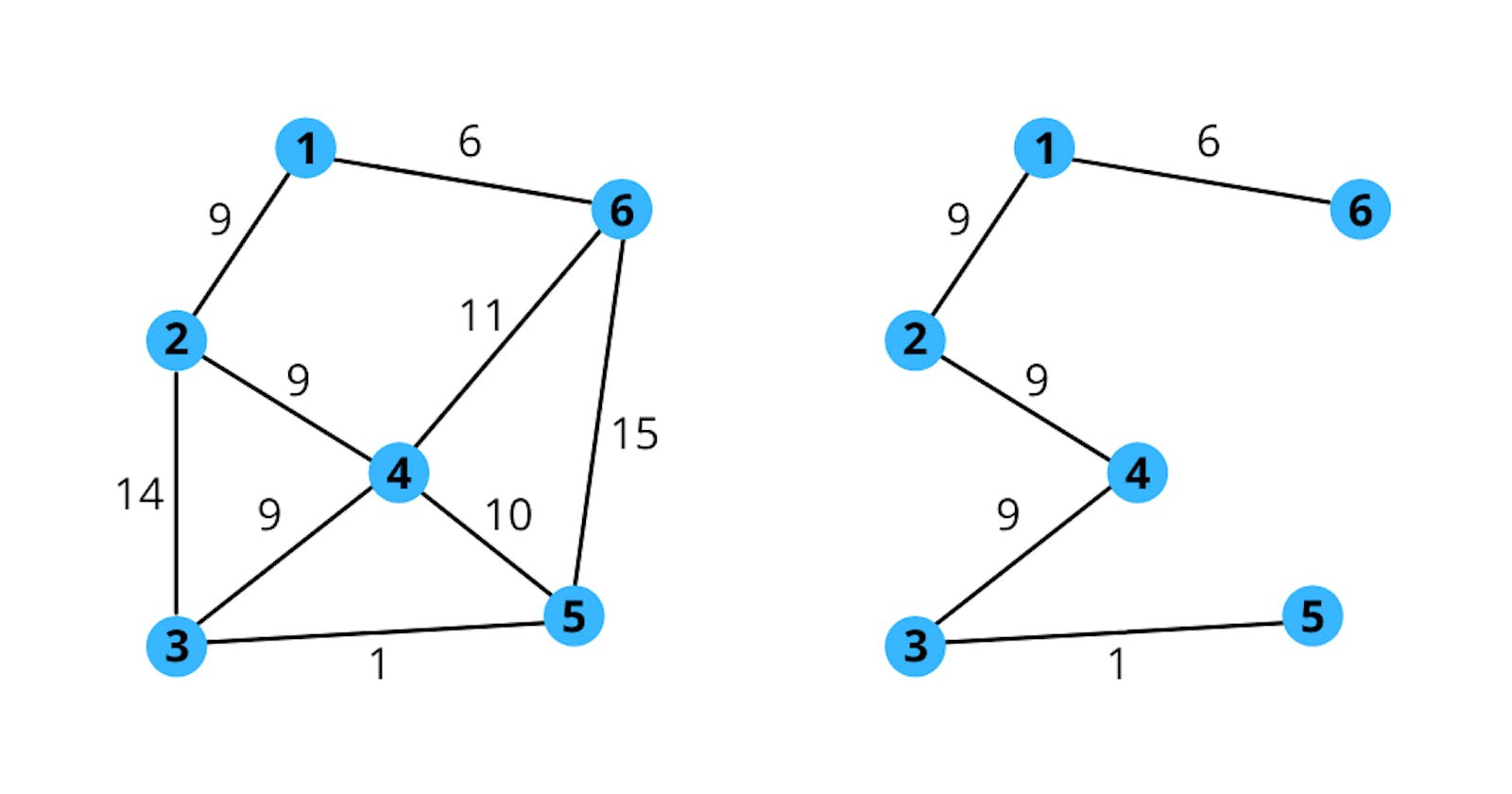
Graph Theory

A graph is a non-linear data structure consisting of nodes (also called as vertices) and edges to connect those nodes. Graphs are used to solve many real world problems and so it is a very important data structure. There are a lot of major algorithms associated with graph and one of them is Kruskal's Minimum Spanning Tree. We will need an undirected weighted graph since minimum spanning tree only exists for such graphs. Consider the graph below.

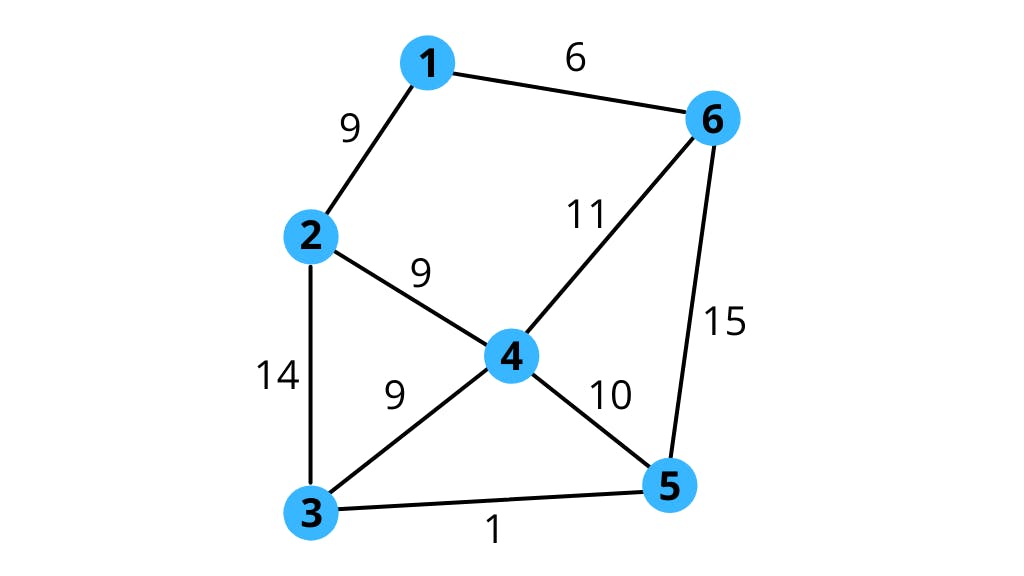
Spanning Tree

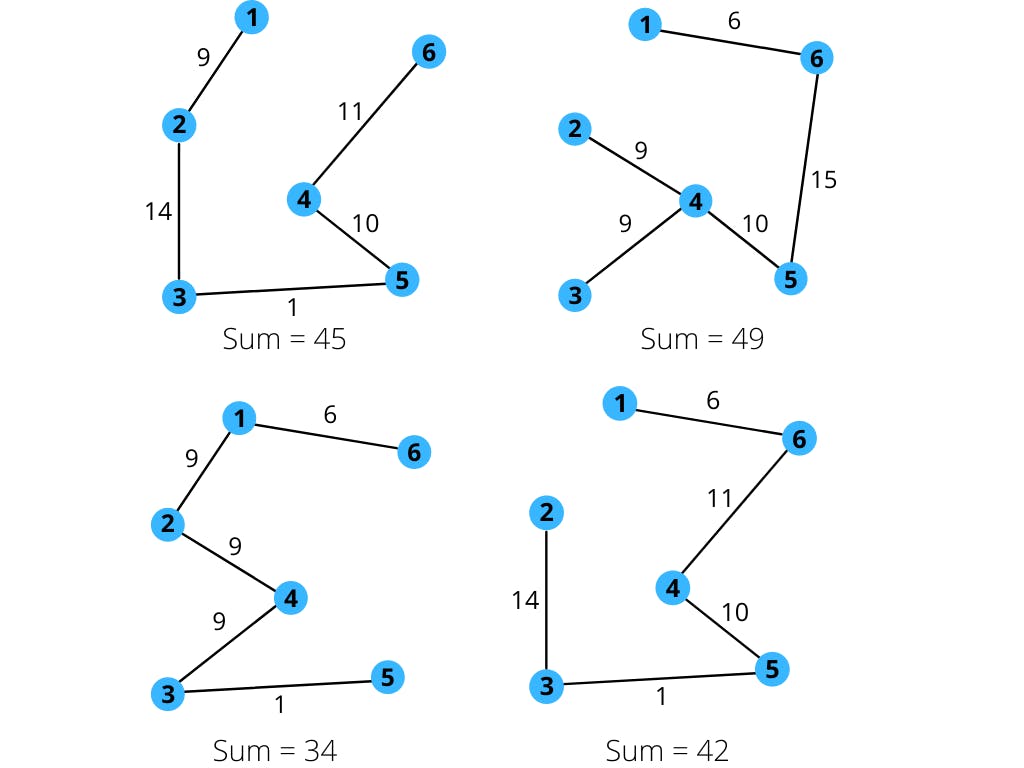
The structure formed when maximum edges are removed from a graph such that the nodes are still connected is called a spanning tree. If a spanning tree has n nodes then it will have n-1 edges. Following are some of the possible spanning trees with their sum of edges of the given graph.

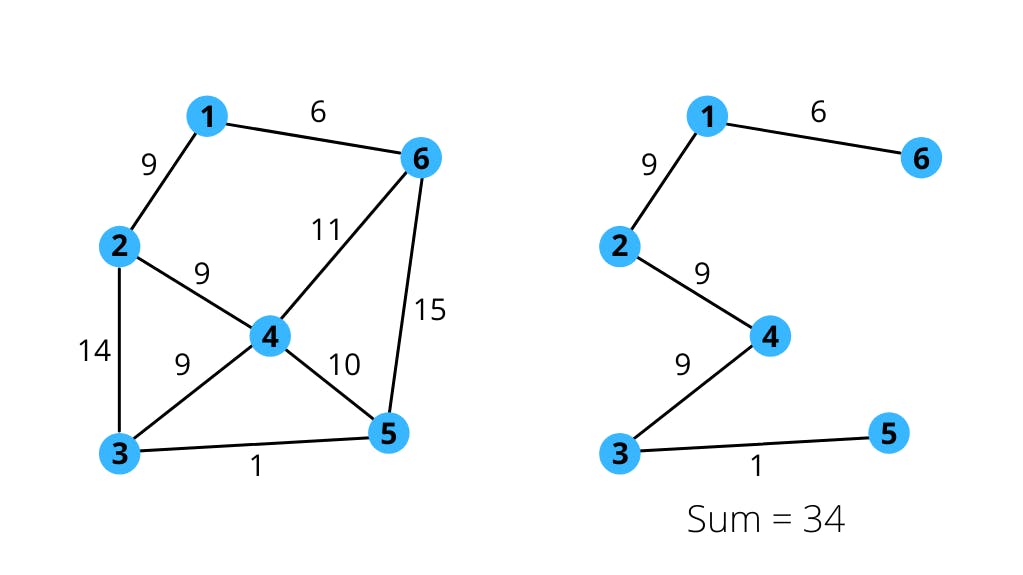
Minimum Spanning Tree

The spanning tree of the graph which has minimum sum of all its edges is called minimum spanning tree. The minimum spanning tree of the given graph is this -

Algorithm

Kruskal's algorithm helps us in finding this minimum spanning tree. It is a greedy based algorithm. Additionally, we also have to use disjoint set data structure. The steps are as follows :-

1. Take all the edges and sort them on the basis of weights.
2. Create disjoint set array for all the nodes. Initially all the nodes are disconnected. We will connect the nodes edge by edge.
3. Iterate over the sorted edges and for each edge check whether the two nodes are already connected or not. If they are not connected, connect them otherwise do nothing. Use the disjoint set union and find concept to check and connect the nodes.

Code

I've used vector of arrays to store edges and their weights for ease of sorting the edges. You can use any data structure but accordingly you have to make changes for sorting.

#include <bits/stdc++.h>
using namespace std;

vector<array<int, 3>> edges;
int parent[10001];

int find(int node) {
    if (parent[node] == node) return node;
    return parent[node] = find(parent[node]);
}

void merge(int a, int b) {
    parent[a] = b;
}

int main() {
    int n, e;
    cin >> n >> e;
    for (int i = 1; i <= e; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        edges.push_back({ w, a, b });
    }

    sort(edges.begin(), edges.end());
    for (int i = 1; i <= n; i++) {
        parent[i] = i;
    }

    int sum = 0;
    for (auto e : edges) {
        int a = find(e[1]);
        int b = find(e[2]);
        if (a != b) {
            sum += e[0];
            merge(a, b);
        }
    }

    cout << sum;
}

The output of the above code for the given graph is 34.

So to conclude, Kruskal's algorithm is very useful in finding the minimum spanning tree. There is also another algorithm called Prim's algorithm which uses priority queue instead of disjoint set but that's for another article.